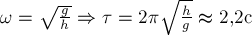ДИНАМИКА
Оглавление
§1. Введение
В динамике изучается механическое движение тел в связи с причинами, вызывающими тот или иной его характер. Напомним, что механическое движение тел относительно и, следовательно, для его описания необходимо указать систему отсчёта, относительно которой рассматривается это движение. При этом система координат выбирается из соображений удобства. Наиболее привычной для нас является декартова прямоугольная система координат.
С целью упрощения начального этапа изучения механического движения принято рассматривать движение не самих реальных тел, а их моделей. Здесь мы будем использовать модель материальной точки.
Определение 1. Материальная точка – это тело, геометрическими размерами которого в условиях конкретной задачи можно пренебречь и считать его геометрической точкой.
Модель материальной точки применима прежде всего в случаях, когда размеры тела намного меньше других характерных размеров в условии задачи. Однако часто в случаях, когда тело движется поступательно, не вращаясь, его можно считать материальной точкой независимо от размеров, формы и пройденного им пути.
Здесь под «телом» мы будем всегда понимать материальную точку (исключая тем самым из рассмотрения вращения тел вокруг собственных осей и изменения форм тел при взаимодействиях). И только из соображений удобства будем на рисунках изображать тела конечных (не точечных) геометрических размеров. Кроме того, при решении задач и на рисунках мы не будем уточнять конкретные точки приложения сил, действующих на тело (или тела) В рамках применяемой модели важно лишь, к какому телу приложены силы, так как тело считается «точкой», и силы, действующие на него приложены к одной этой «точке». На рисунках, однако, бывает удобно пространственно разнести точки приложения сил, действующих на конкретное тело, не выходя за пределы контура, изображающего это тело.
§2. 1-й закон Ньютона. Инерциальные системы отсчёта.
На всякое тело могут оказывать воздействия другие тела, его окружающие, в результате чего может измениться состояние движения (покоя) наблюдаемого тела. Вместе с тем такие воздействия могут быть скомпенсированы (уравновешены) и не вызывать таковых изменений.
1-й закон Ньютона (закон инерции):тело находится в состоянии покоя или равномерного прямолинейного движения - движения по инерции - до тех пор, пока воздействия со стороны других тел не выведут его из этого состояния.
Применительно к сказанному, изменение скорости тела (т.е. ускорение) всегда вызывается воздействием на это тело каких-либо других тел.
1-й закон Ньютона выполняется в инерциальных система отсчёта.
Определение 2. Системы отсчёта, относительно которых тело, не испытывающее на себе воздействия других тел, покоится или движется равномерно и прямолинейно, называются инерциальными.
Установить, является ли данная система отсчёта инерциальной, можно лишь опытным путём. В большинстве случаев можно считать инерциальными системы отсчёта, связанные с Землёй или с телами отсчёта, которые по отношению к земной поверхности движутся равномерно и прямолинейно.
Если тело отсчёта движется с ускорением, то связанная с ним система отсчёта является неинерциальной, и в ней 1-й закон Ньютона несправедлив. Мы будем рассматривать явления только в инерциальных системах отсчёта.
Пример 1. В каком из приведённых ниже случаев речь идёт о движении тела по инерции? Выберите правильный вариант ответа.
ОТВЕТ. Правильный вариант 1).
Действительно, движение по инерции происходит равномерно и прямолинейно. В случае 2) движение неравномерное, а в случае 3) – непрямолинейное.
Определение 3. Свойство тел сохранять во времени своё состояние (скорость движения, направление движения, состояние покоя и т.п.) называют инертностью.
С проявлением инертности тел мы часто встречаемся в повседневности. При резком торможении автобуса пассажиры, находящиеся в нём, наклоняются вперёд, а при повороте автобуса вправо – к левой его стенке. При большом ускорении взлетающего самолёта тело пилота, стремясь сохранить первоначальное состояние покоя, прижимается к сидению.
Инертность тела принято характеризовать его массой (инертной массой).
Определение 4. Масса - скалярная физическая величина, являющаяся мерой инертности тела.
Единицей измерения массы в системе СИ служит килограмм (кг).
§3. Взаимодействие тел. Сила.
Любое действие тел друг на друга носит характер взаимодействия, то есть, если тело А действует на тело В, то всегда одновременно тело В действует на тело А, причём непосредственный контакт между телами необязателен. В результате взаимодействия тела могут сообщать друг другу ускорения (изменять состояния покоя или движения).
Определение 5.Силой называется векторная физическая величина, являющаяся мерой взаимодействия тел.
Сила характеризуется 1) направлением, 2) модулем
(величиной) и 3) точкой приложения (тело, к которому она приложена).
Сила обозначается через 
Модуль силы обозначается как 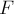 . Единицей измерения силы в системе СИ служит ньютон (Н).
. Единицей измерения силы в системе СИ служит ньютон (Н).
Если
на тело одновременно действуют несколько сил 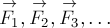 то бывает удобно заменить их равнодействующей силой.
то бывает удобно заменить их равнодействующей силой.
Определение 6. Сила, которая производит на тело такое же действие, как и несколько одновременно действующих сил, называется равнодействующей.
§4. Нахождение равнодействующей.
Нахождение равнодействующей  нескольких
сил
нескольких
сил 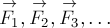 осуществляется с помощью правил векторного
сложения:
осуществляется с помощью правил векторного
сложения: 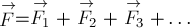 .
.
Пример 2.
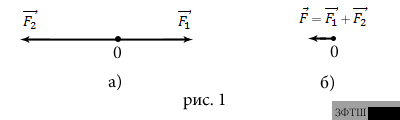
Две силы 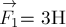 и
и 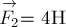 приложены к одной точке и направлены вдоль одной прямой в противоположные стороны (рис.1а). Найдите их равнодействующую.
приложены к одной точке и направлены вдоль одной прямой в противоположные стороны (рис.1а). Найдите их равнодействующую.
ОТВЕТ. Модуль равнодействующей равен разности
модулей 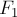 и
и 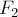 , то есть
, то есть 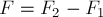 .
Равнодействующая приложена в той же точке и направлена в сторону большей по модулю силы
.
Равнодействующая приложена в той же точке и направлена в сторону большей по модулю силы 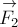 (рис.1б).
(рис.1б).
Пример 3.
Две силы 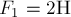 и
и 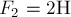 приложены к одной точке О и направлены под углом
приложены к одной точке О и направлены под углом 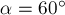 друг к другу (рис.2). Найдите их равнодействующую.
друг к другу (рис.2). Найдите их равнодействующую.
ОТВЕТ. Согласно правилу параллелограмма,
равнодействующая определяется диагональю параллелограмма, построенного на
векторах 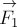 и
и 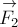 как на сторонах (рис.2б). В нашем
случае модуль равнодействующей найдём по теореме косинусов:
как на сторонах (рис.2б). В нашем
случае модуль равнодействующей найдём по теореме косинусов: 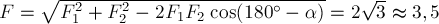 Направление равнодействующей
определим посредством угла
Направление равнодействующей
определим посредством угла 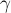 , который равнодействующая
составляет с одной из заданных сил, например – с
, который равнодействующая
составляет с одной из заданных сил, например – с 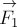 . В нашем случае
по теореме синусов
. В нашем случае
по теореме синусов 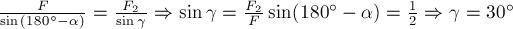 .
Точка приложения равнодействующей совпадает с точкой приложения исходных сил.
.
Точка приложения равнодействующей совпадает с точкой приложения исходных сил.
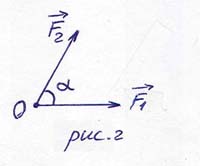
Замечание.
Вместо правила параллелограмма при сложении двух векторов часто пользуются
правилом треугольника. Для рассмотренного выше примера 4 векторный треугольник
будет иметь вид, как на рис.3, и угол 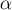 между направлениями действия
сил будет являться внешним углом треугольника.
между направлениями действия
сил будет являться внешним углом треугольника.
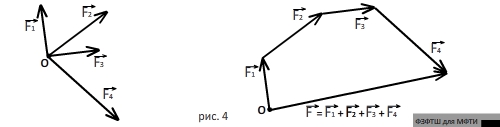
Если нужно сложить более двух сил, приложенных в
одной точке, то пользуются правилом многоугольника: из конца первой силы
проводят вектор, равный и параллельный второй силе; из конца второй силы –
вектор, равный и параллельный третьей силе и так далее. Замыкающий вектор,
проведённый из точки приложения сил к концу последней силы, по величине и
направлению равен равнодействующей. На рис.4 это правило проиллюстрировано на
примере нахождения равнодействующей  четырёх сил
четырёх сил 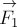 ,
, 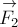 ,
, 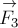 и
и 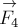 . Заметим, что при этом складываемые векторы не
обязательно должны принадлежать одной плоскости.
. Заметим, что при этом складываемые векторы не
обязательно должны принадлежать одной плоскости.
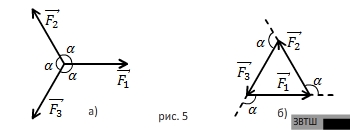
Пример 4.
Три одинаковые по модулю
силы 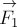 ,
, 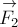 и
и 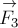 приложены к одной точке, лежат в одной
плоскости и направлены под одинаковыми углами
приложены к одной точке, лежат в одной
плоскости и направлены под одинаковыми углами 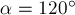 попарно
друг к другу (рис.5а). Найдите их равнодействующую.
попарно
друг к другу (рис.5а). Найдите их равнодействующую.
ОТВЕТ. Равнодействующая этих сил равна нулю. Действуя по правилу многоугольника, получим на
чертеже (рис.5б) замкнутый треугольник сил 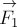 ,
, 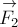 и
и 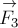 , и
замыкающий вектор будет нулевым.
, и
замыкающий вектор будет нулевым.
Пример 5.
Три силы 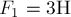 ,
, 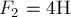 и
и 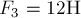 приложены в одной точке и направлены взаимно
перпендикулярно друг другу (силы
приложены в одной точке и направлены взаимно
перпендикулярно друг другу (силы 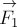 и
и 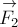 лежат в
горизонтальной плоскости, а сила
лежат в
горизонтальной плоскости, а сила 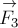 направлена вертикально) (рис.6).
Найдите равнодействующую.
направлена вертикально) (рис.6).
Найдите равнодействующую.
ОТВЕТ. Сложение по правилу многоугольника
даёт результат, изображённый на рис.6. Видим, что равнодействующая  представляет собой диагональ параллелепипеда,
построенного на векторах
представляет собой диагональ параллелепипеда,
построенного на векторах 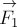 ,
, 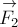 и
и 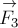 как на
рёбрах. Модуль равнодействующей, следовательно, равен
как на
рёбрах. Модуль равнодействующей, следовательно, равен 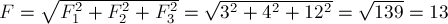 .
Направление равнодействующей определим с помощью
углов
.
Направление равнодействующей определим с помощью
углов 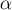 и
и 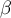 . Из рис.6б видим, что эти углы таковы, что
. Из рис.6б видим, что эти углы таковы, что 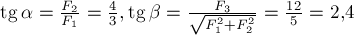 .
Точка приложения равнодействующей совпадает с точкой приложения исходных сил.
.
Точка приложения равнодействующей совпадает с точкой приложения исходных сил.
В ряде случаев удобнее производить сложение векторов «методом проекций».
Пример 6.
Три силы 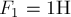 ,
, 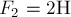 и
и 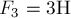 приложены к одной точке
приложены к одной точке 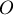 , лежат в вертикальной плоскости и составляют углы
, лежат в вертикальной плоскости и составляют углы 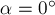 ,
,
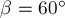 и
и 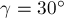 с
горизонталью соответственно (рис.7а). Найдите равнодействующую этих сил.
с
горизонталью соответственно (рис.7а). Найдите равнодействующую этих сил.
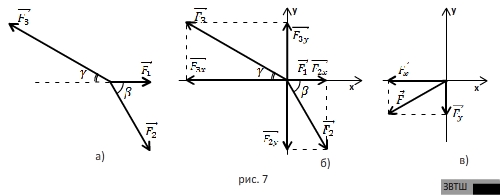
ОТВЕТ. Проведём две взаимно
перпендикулярные оси  и
и  так, чтобы ось
так, чтобы ось  совпадала с
горизонталью, вдоль которой направлена сила
совпадала с
горизонталью, вдоль которой направлена сила 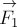 .
Спроецируем данные силы на оси координат (рис.7б).
Проекции
.
Спроецируем данные силы на оси координат (рис.7б).
Проекции 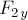 и
и 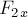 отрицательны.
Сумма проекций всех сил на оси
отрицательны.
Сумма проекций всех сил на оси 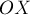 равна проекции на эту ось равнодействующей
равна проекции на эту ось равнодействующей 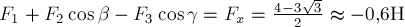 .
Аналогично для проекций на ось
.
Аналогично для проекций на ось 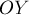 :
: 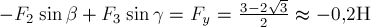 .
Модуль равнодействующей определяется по теореме Пифагора:
.
Модуль равнодействующей определяется по теореме Пифагора: 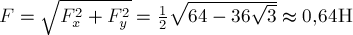 .
Направление равнодействующей определим с помощью угла
.
Направление равнодействующей определим с помощью угла 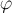 , который составляет вектор равнодействующей и осью
, который составляет вектор равнодействующей и осью 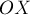 (рис.7в):
(рис.7в): 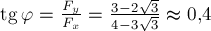
§5. Разложение силы на составляющие
Для решения многих задач бывает необходимо рассмотреть обратную ситуацию – найти несколько сил, которые своим совместным действием могли бы заменить одну данную силу. Такие силы называются составляющими, а сама операция называется разложением сил на составляющие. В качестве иллюстрации рассмотрим частные случаи разложения силы на две составляющие, когда и сила, и её составляющие лежат в одной плоскости.
Задачу разложения силы на две составляющие можно решить, пользуясь правилом параллелограмма, причём исходная сила рассматривается как его диагональ. Но параллелограммов с одинаковой заданной диагональю можно построить сколь угодно много (рис.8).
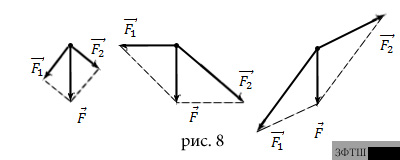
Для того, чтобы задача стала определённой и решалась однозначно, необходимо кроме заданной силы указать одно из следующих условий:
Пример 7.
Сила 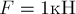 приложена в
точке В кронштейна и направлена вертикально вниз (рис.9а). Найдите
составляющие этой силы по направлениям стержней кронштейна. Необходимые данные
указаны на рисунке.
приложена в
точке В кронштейна и направлена вертикально вниз (рис.9а). Найдите
составляющие этой силы по направлениям стержней кронштейна. Необходимые данные
указаны на рисунке.
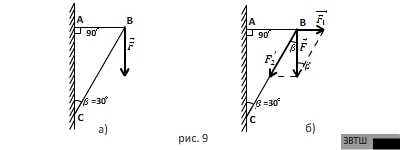
РЕШЕНИЕ. Пусть стержни прикреплены к стене в
точках 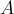 и
и 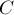 . Разложение силы
. Разложение силы  на составляющие вдоль направлений
на составляющие вдоль направлений 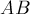 и
и
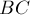 представлено на рис.9б. Откуда видно, что
представлено на рис.9б. Откуда видно, что 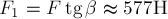 ;
; 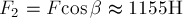 .
.
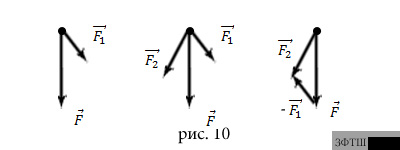
Пример 8.
Дана сила  и её
составляющая сила
и её
составляющая сила 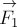 (рис.10а). Найдите вторую составляющую
силы
(рис.10а). Найдите вторую составляющую
силы 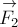 .
.
РЕШЕНИЕ. Задача сводится к построению
параллелограмма по диагонали и одной из сторон, известному из планиметрии. На
рис.10б построен такой параллелограмм и указана искомая
составляющая 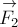 силы
силы 
Второй способ решения: прибавить к силе 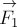 силу, равную
силу, равную 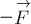 (рис.10в).
(рис.10в).
В результате получим искомую силу 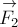 .
.
§6. Второй закон Ньютона
Второй закон Ньютона утверждает, что в
инерциальных системах отсчёта ускорение 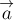 тела прямо пропорционально
равнодействующей
тела прямо пропорционально
равнодействующей  всех приложенных к телу сил и обратно
пропорционально массе тела:
всех приложенных к телу сил и обратно
пропорционально массе тела: 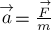
В более удобном виде можно записать: 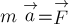 (1)
(1)
Видим, что векторы  и
и 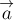 коллинеарные
и, так как масса тела – величина положительная, то направления этих векторов
одинаковы. В свою очередь направления скорости тела и перемещения тела могут не
совпадать с направлением вектора
коллинеарные
и, так как масса тела – величина положительная, то направления этих векторов
одинаковы. В свою очередь направления скорости тела и перемещения тела могут не
совпадать с направлением вектора  .
.
Учитывая, что по определению
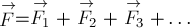 (см. выше),
выражение (1) можно написать в виде:
(см. выше),
выражение (1) можно написать в виде:
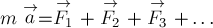 (1.1)
(1.1)
после чего его можно переписать для проекций ускорения и сил на оси выбранной системы координат.
Если все силы, действующие на тело, лежат в одной плоскости, то можно
ограничиться двумя координатными осями 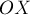 и
и 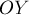 . Тогда получим систему
двух скалярных уравнений
. Тогда получим систему
двух скалярных уравнений 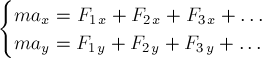 (1.2)
равносильную одному векторному уравнению (1.1).
(1.2)
равносильную одному векторному уравнению (1.1).
Пример 9.
Тело, массой 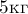 движется с
ускорением
движется с
ускорением 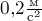 . Выберите правильное утверждение.
. Выберите правильное утверждение.
ОТВЕТ. Верно утверждение 3).
Действительно, в соответствии с выражением (1)
модуль равнодействующей равен произведению массы тела на модуль ускорения. В
нашем случае это произведение равно 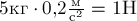 .
.
Пример 10.
Под действием силы 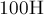 тело
движется прямолинейно вдоль оси
тело
движется прямолинейно вдоль оси 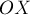 так, что его координата изменяется со
временем по закону
так, что его координата изменяется со
временем по закону 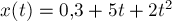 . Какова масса тела?
. Какова масса тела?
РЕШЕНИЕ. Видим, что зависимость 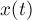 соответствует случаю равноускоренного движения. Следовательно, коэффициент
при
соответствует случаю равноускоренного движения. Следовательно, коэффициент
при 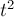 равен половине проекции ускорения тела на ось
равен половине проекции ускорения тела на ось 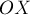 . Таким
образом, в нашем случае
. Таким
образом, в нашем случае 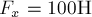 ,
, 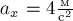 и,
значит,
и,
значит, 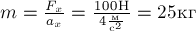 .
.
Пример 11.
На тело массой 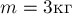 действуют сила
действуют сила 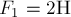 под
углом
под
углом 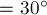 к оси
к оси 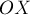 и сила
и сила 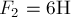 под углом
под углом 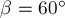 к оси
к оси 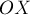 (рис.11а). Найдите проекции ускорения тела на оси
(рис.11а). Найдите проекции ускорения тела на оси 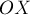 и
и 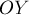 и само ускорение тела.
и само ускорение тела.
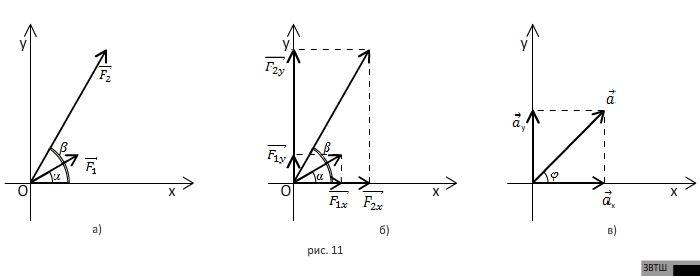
РЕШЕНИЕ. В данном случае система уравнений (1.2) имеет вид (рис.11б):
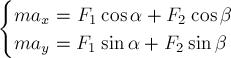
Отсюда получаем
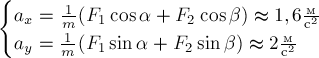
Модуль ускорения равен
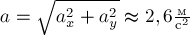 .
.
Направление ускорения тела определим с помощью угла 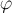 между вектором ускорения и осью
между вектором ускорения и осью 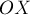 (рис.11в).
Угол
(рис.11в).
Угол 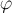 таков, что
таков, что 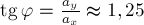 .
.
§7. Импульс материальной тоски.
Другая формулировка 2-го закона Ньютона.
Определение 7.
Импульсом 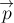 материальной
точки называется векторная величина, равная произведению массы материальной
точки на её скорость:
материальной
точки называется векторная величина, равная произведению массы материальной
точки на её скорость: 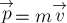
Видим, что векторы импульса и скорости коллинеарные
и сонаправленные. Единицей измерения импульса в системе СИ служит 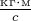 (для этой единицы нет специального
названия).
(для этой единицы нет специального
названия).
Пример 12.
Камень массой 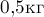 брошен вертикально вверх с начальной скоростью
брошен вертикально вверх с начальной скоростью 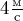 . Укажите все правильные утверждения.
. Укажите все правильные утверждения.
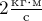 и направлен вертикально вверх.
и направлен вертикально вверх.ОТВЕТ. Верно утверждение 1) и 3).
Действительно, произведение
массы тела на модуль его скорости даёт 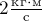 ,
а направление импульса совпадает с направлением скорости. Далее, с изменением
скорости камня изменяется и его импульс. При движении вверх направление скорости
остаётся неизменным, а модуль скорости уменьшается. Следовательно, и импульс
камня, сохраняя своё направление, уменьшается по модулю.
,
а направление импульса совпадает с направлением скорости. Далее, с изменением
скорости камня изменяется и его импульс. При движении вверх направление скорости
остаётся неизменным, а модуль скорости уменьшается. Следовательно, и импульс
камня, сохраняя своё направление, уменьшается по модулю.
Если масса  тела остаётся постоянной, а его
скорость
тела остаётся постоянной, а его
скорость 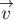 изменяется, то приращение
изменяется, то приращение 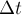 импульса тела
равно:
импульса тела
равно: 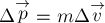 .
Используя определение ускорения тела и
учитывая выражение (1), можно заключить, что в течение некоторого малого (!)
промежутка времени
.
Используя определение ускорения тела и
учитывая выражение (1), можно заключить, что в течение некоторого малого (!)
промежутка времени 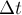 справедливо равенство или:
справедливо равенство или:
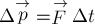 (2)
(2)
Определение 8.
Векторная величина 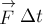 ,
численно равная произведению силы
,
численно равная произведению силы  на
время её действия
на
время её действия 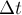 , называется импульсом силы.
, называется импульсом силы.
Импульс силы мы будем обозначать через 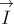 .
.
В системе СИ импульс силы измеряется в 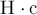 или,
что то же, в
или,
что то же, в 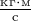 .
.
Приращение импульса тела – это вектор, направление
которого совпадает с направлением силы  , действующей на тело и
вызывающей изменение его скорости (т.е. ускорение). Таким образом, в
инерциальных системах отсчёта можно сформулировать 2-й закон Ньютона в виде
(2):
приращение импульса тела прямо
пропорционально импульсу силы
, действующей на тело и
вызывающей изменение его скорости (т.е. ускорение). Таким образом, в
инерциальных системах отсчёта можно сформулировать 2-й закон Ньютона в виде
(2):
приращение импульса тела прямо
пропорционально импульсу силы  и происходит по направлению
силы
и происходит по направлению
силы  .
.
Если равнодействующая сила  постоянна (не
изменяется во времени), то из (2) можно непосредственно найти приращение
импульса тела за любой, уже не обязательно малый (!), промежуток
времени
постоянна (не
изменяется во времени), то из (2) можно непосредственно найти приращение
импульса тела за любой, уже не обязательно малый (!), промежуток
времени 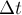 :
:
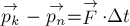
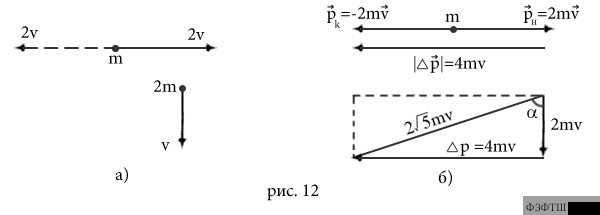
Пример 13.
На две материальные точки
массами  и
и 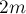 ,движущиеся во взаимно перпендикулярных
направлениях со скоростями
,движущиеся во взаимно перпендикулярных
направлениях со скоростями 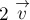 и
и 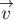 соответственно
(рис.12а), в течение некоторого одинакового промежутка времени действуют
одинаковые по модулю и направлению силы. В момент прекращения действия сил
первая точка движется в обратном направлении с той же скоростью
соответственно
(рис.12а), в течение некоторого одинакового промежутка времени действуют
одинаковые по модулю и направлению силы. В момент прекращения действия сил
первая точка движется в обратном направлении с той же скоростью 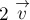 (как
показано пунктиром на рис.12б). Определите модуль и направление скорости
второй материальной точки (массой
(как
показано пунктиром на рис.12б). Определите модуль и направление скорости
второй материальной точки (массой 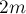 ) в этот момент времени.
) в этот момент времени.
РЕШЕНИЕ. Импульсы сил, действующих на
материальные точки, одинаковы. Следовательно, одинаковы и приращения импульсов
точек. Модуль приращения импульса первой из них
равен 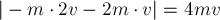 . Вектор
. Вектор 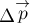 направлен
горизонтально (рис.12б). Конечный импульс второй материальной точки равен сумме
еёначального импульса и вектора
направлен
горизонтально (рис.12б). Конечный импульс второй материальной точки равен сумме
еёначального импульса и вектора 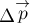 (рис.12б). Модуль конечного
импульса найдём по теореме Пифагора:
(рис.12б). Модуль конечного
импульса найдём по теореме Пифагора: 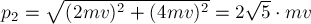 , а
скорость материальной точки равна
, а
скорость материальной точки равна 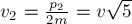 .
Направление вектора скорости составляет угол
.
Направление вектора скорости составляет угол 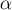 с
направлением начального импульса этой материальной точки, причём
с
направлением начального импульса этой материальной точки, причём 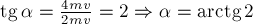 .
.
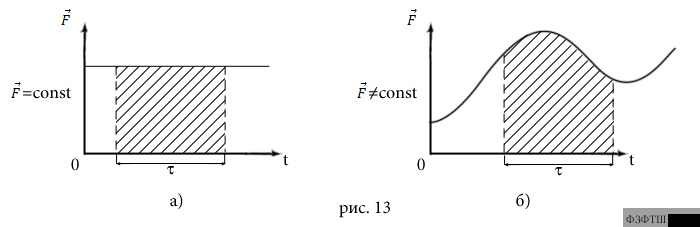
В случае, когда сила  постоянная, график
зависимости модуля
постоянная, график
зависимости модуля 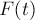 от времени имеет вид прямой, параллельной оси
абсцисс (рис.13а), а модуль импульса силы за произвольный промежуток
времени
от времени имеет вид прямой, параллельной оси
абсцисс (рис.13а), а модуль импульса силы за произвольный промежуток
времени 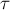 численно равен площади прямоугольника, заштрихованного на
рисунке. Этому же раве н и модуль приращения импульса тела.
численно равен площади прямоугольника, заштрихованного на
рисунке. Этому же раве н и модуль приращения импульса тела.
Если же равнодействующая сила  изменяется
по модулю с течением времени, то график зависимости
изменяется
по модулю с течением времени, то график зависимости 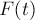 может иметь
произвольную форму, соответствующую конкретным условиям. Однако и в общем
случае модуль импульса такой силы (а, значит, и модуль приращения импульса
тела) за произвольный промежуток времени
может иметь
произвольную форму, соответствующую конкретным условиям. Однако и в общем
случае модуль импульса такой силы (а, значит, и модуль приращения импульса
тела) за произвольный промежуток времени 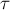 численно равен площади
под графиком
численно равен площади
под графиком 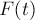 (рис.13б).
(рис.13б).
Пример 14.
Тело движется под действием постоянной
силы 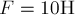 Чему равно приращение импульса тела за 1 мин
действия этой силы?
Чему равно приращение импульса тела за 1 мин
действия этой силы?
РЕШЕНИЕ. Сила постоянная. График
зависимости 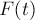 имеет вид, как на рис.13а, где надо
положить
имеет вид, как на рис.13а, где надо
положить 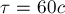 . Модуль импульса силы численно равен площади
под графиком
. Модуль импульса силы численно равен площади
под графиком 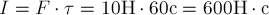
Тому же равен модуль 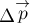 приращения
импульса тела. Направление вектора
приращения
импульса тела. Направление вектора 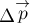 совпадает с направлением
силы
совпадает с направлением
силы  .
.
Пример 15.
Тело массы 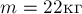 движется прямолинейно со скоростью
движется прямолинейно со скоростью 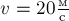 .
В момент времени
.
В момент времени 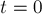 на
него начинает действовать тормозящая сила
на
него начинает действовать тормозящая сила  , направленная в
противоположную сторону, модуль которой увеличивается со временем по линейному
закону (рис.14). Через какое время
, направленная в
противоположную сторону, модуль которой увеличивается со временем по линейному
закону (рис.14). Через какое время 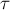 скорость тела уменьшится
до
скорость тела уменьшится
до 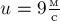 ?
?
РЕШЕНИЕ. Модуль приращения импульса тела
равен 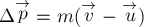 .
Направление вектора
.
Направление вектора 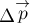 противоположно направлению начального импульса тела.
Модуль импульса силы тоже должен быть равен
противоположно направлению начального импульса тела.
Модуль импульса силы тоже должен быть равен 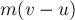 . С другой
стороны он равен площади под графиком на промежутке времени от
. С другой
стороны он равен площади под графиком на промежутке времени от 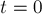 до
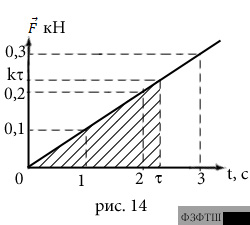
до 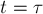 (рис.14). По условию зависимость модуля тормозящей силы от
времени имеет вид
(рис.14). По условию зависимость модуля тормозящей силы от
времени имеет вид 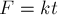 , где
, где 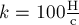 - тангенс угла наклона
графика к оси абсцисс. Площадь прямоугольного треугольника со
сторонами
- тангенс угла наклона
графика к оси абсцисс. Площадь прямоугольного треугольника со
сторонами 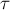 и
и 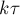 равна
равна 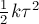 . Таким
образом
. Таким
образом 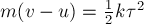
Откуда находим 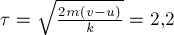 .
.
В рамках школьной программы площадь под
графиком 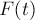 на рис.13б подсчитать порой довольно сложно.
Тогда часто вводят понятие средней (по модулю) силы.
на рис.13б подсчитать порой довольно сложно.
Тогда часто вводят понятие средней (по модулю) силы.
Пример 16.
Футболист бьёт по мячу
массой 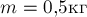 , лежащему на поверхности земли. После удара мяч
улетает со скоростью
, лежащему на поверхности земли. После удара мяч
улетает со скоростью 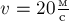 .
Длительность удара
.
Длительность удара 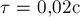 . Чему равна средняя сила удара футболиста по мячу?
Действием других сил за время удара пренебречь.
. Чему равна средняя сила удара футболиста по мячу?
Действием других сил за время удара пренебречь.
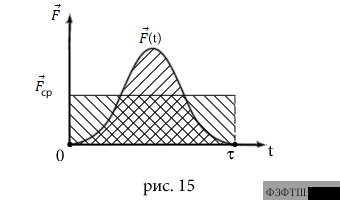
РЕШЕНИЕ. Качественная зависимость модуля силы, действующей на мяч при ударе, от времени показана на рис.15. Однако практически никогда конкретный аналитический вид такой зависимости неизвестен.
Заменим реальную силу 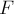 средней постоянной
во времени силой
средней постоянной
во времени силой 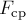 так, чтобы её импульс за промежуток
времени
так, чтобы её импульс за промежуток
времени 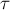 был равен импульсу реальной силы за то же время.
Графически это выражается в том, что площадь под графиками зависимостей
реальной силы
был равен импульсу реальной силы за то же время.
Графически это выражается в том, что площадь под графиками зависимостей
реальной силы 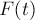 и силы
и силы 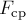 на отрезке времени
на отрезке времени 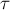 одинаковы и равны
одинаковы и равны 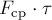 .
.
Поскольку первоначально мяч покоился, его начальный
импульс равен нулю. После удара мяч приобретает импульс 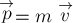 и,
следовательно, приращение импульса мяча за время удара равно
и,
следовательно, приращение импульса мяча за время удара равно 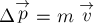 .
Для модулей приращения импульса мяча и импульса силы имеем:
.
Для модулей приращения импульса мяча и импульса силы имеем: 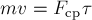 (по условию действием других сил
за время
(по условию действием других сил
за время 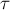 пренебрегаем). Отсюда искомая средняя (по времени) сила удара
по мячу равна:
пренебрегаем). Отсюда искомая средняя (по времени) сила удара
по мячу равна: 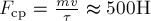 .
.
§8. Третий закон Ньютона
Третий закон Ньютона утверждает, что в инерциальных системах отсчёта независимо от того движутся взаимодействующие тела или находятся в относительном покое; силы, с которыми два тела действуют друг на друга, равны по модулю, противоположны по направлению и приложены соответственно к взаимодействующим телам.
Если тело А действует на тело В с
силой 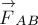 (рис.16), то одновременно на тело В со стороны тале А
будет действовать сила
(рис.16), то одновременно на тело В со стороны тале А
будет действовать сила 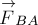 , причём
, причём
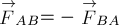 (3)
(3)
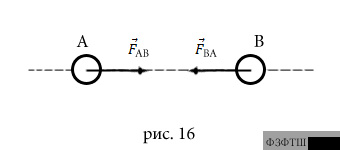
Силы взаимодействия приложены к разным телам и, следовательно не могут уравновешиваться. Их нельзя складывать или вычитать.
3-й закон Ньютона распространяется и на систему из произвольного числа взаимодействующих тел. Просто в этом случае следует рассматривать силы попарного взаимодействия между телами системы.
ПРИМЕР 17. Мяч ударяется о стенку. На какое из тел (мяч или стенку) действует при ударе бóльшая сила? Выберите правильное утверждение.
ОТВЕТ. Правильные вариант 3). По 3-му закону Ньютона первые два варианта отпадают.
ПРИМЕР 18.
В результате взаимодействия двух тел
массами 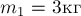 и
и 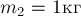 первое тело приобрело
ускорение
первое тело приобрело
ускорение 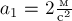 . Чему равно ускорение
. Чему равно ускорение 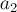 , приобретённое
вторым телом?
, приобретённое
вторым телом?
РЕШЕНИЕ. По 3-му закону Ньютона силы, с
которыми взаимодействуют тела удовлетворяют равенству (3). С учётом 2-го закона
Ньютона это равенство можно переписать в виде:
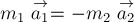 .
Отсюда для модулей ускорений тел следует, что
.
Отсюда для модулей ускорений тел следует, что 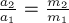 .
Из этого равенства легко находим
.
Из этого равенства легко находим 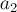 :
: 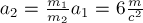 ;
Направление ускорения
;
Направление ускорения 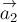 противоположно направлению ускорения
противоположно направлению ускорения 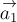
§9. Закон всемирного тяготения. Сила тяжести.
В соответствии с законом всемирного тяготения
сила гравитационного притяжения между двумя материальными точками прямо
пропорциональна произведению масс 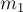 и
и 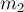 точек, обратно
пропорциональна квадрату расстояния между ними и направлена по прямой, их
соединяющей:
точек, обратно
пропорциональна квадрату расстояния между ними и направлена по прямой, их
соединяющей: 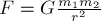 (4),
где
(4),
где 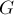 - гравитационная постоянная,
- гравитационная постоянная, 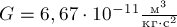
Можно показать, что однородные тела шарообразной
формы, даже если их размеры не малы по сравнению с расстоянием между ними,
также взаимодействуют с гравитационными силами, определяемыми формулой (4),
где 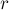 -расстояние между центрами шаров, а силы направлены вдоль прямой,
соединяющей центры шаров.
-расстояние между центрами шаров, а силы направлены вдоль прямой,
соединяющей центры шаров.
ПРИМЕР 19. Два одинаковых однородных шара притягиваются друг к другу с некоторой силой. Массу каждого шара увеличили втрое. Выберите правильное утверждение.
ОТВЕТ. Верный вариант 2).
Действительно, по закону всемирного тяготения
гравитационная сила прямо пропорциональна произведению масс тел, а если каждый
из сомножителей увеличить в три раза, то произведение увеличится в 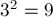 раз.
раз.
Любое тело на поверхности Земли (или другой
планеты) испытывает действие силы гравитационного притяжения к ней. Эта сила
называется силой тяжести и равна 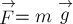 ,
где
,
где  - масса тела,
- масса тела, 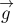 - ускорение свободного падения. Сила тяжести направлена
к центру Земли (неоднородностью Земного шара пренебрегаем).
- ускорение свободного падения. Сила тяжести направлена
к центру Земли (неоднородностью Земного шара пренебрегаем).
Модуль вектора 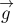 можно определить с
помощью формулы (4). Пренебрегая расстоянием между телом и поверхностью Земли
по сравнению с радиусом Земли
можно определить с
помощью формулы (4). Пренебрегая расстоянием между телом и поверхностью Земли
по сравнению с радиусом Земли 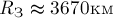 , получим
, получим
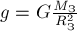 (5),
(5), 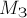 - масса Земли.
- масса Земли.
Пренебрегая отклонением формы Земли от шарообразной,
считают 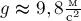 .
.
Аналогичные рассуждения справедливы также и для других планет и космических тел шарообразной формы.
ПРИМЕР 20. Чему равно ускорение сводного падения на поверхности планеты, масса которой в 3 раза больше массы Земли, а радиус в два раза больше радиуса Земли?
РЕШЕНИЕ. В соответствии с (5) искомое
ускорение равно 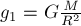 , где
, где 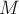 - масса
планеты,
- масса
планеты, 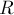 - радиус планеты. По условию
- радиус планеты. По условию 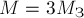 ,
, 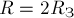 .
Следовательно:
.
Следовательно: 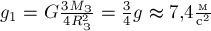 , где
, где 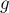 - ускорение
свободного падения на поверхности Земли.
- ускорение
свободного падения на поверхности Земли.
§10. Сила упругости. Закон Гука
Силами упругости обычно называют силы, возникающие при деформации тела и зависящие от величины этой деформации. Под деформацией понимают изменение формы или объёма тела. При этом различные части тела испытывают различные перемещения. Например при растяжении или сжатии пружины больше всего смещаются края пружины, а её середина практически остаётся на месте. Заметим, что при таком рассмотрении деформируемые тела не являются материальными точками. Силы упругости приложены к телу, вызывающему деформацию, и направлены в сторону, противоположную направлению относительного смещения частиц деформируемого тела. Деформируемое тело как бы сопротивляется стремлению его деформировать.
Вместе с тем не всякая деформация приводит к появлению сил упругости. Силы упругости возникают в телах, способных восстанавливать свою форму (или объём) после прекращения действия сил, вызывающих деформацию (упругие тела). Но в то же время существуют и так называемые пластичные тела, которые этим свойством не обладают. При их деформации возникают силы, зависящие от скорости, с которой производится деформация, а не от величины деформации, а это уже - не силы упругости.
Чаще всего при первом ознакомлении с темой
рассматриваются силы упругой деформации, возникающие при растяжении или сжатии
пружины, резинового шнура, верёвки, жёсткого стержня, доски и т.п. При малых
деформациях этих и других тел справедлив закон Гука: модуль силы
упругости 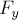 прямо пропорционален модулю деформации тела:
прямо пропорционален модулю деформации тела: 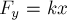 (6),
где
(6),
где 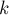 - положительный
коэффициент упругости, зависящий от материала, формы и свойств деформируемого
тела. Величина
- положительный
коэффициент упругости, зависящий от материала, формы и свойств деформируемого
тела. Величина 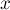 в указанных выше примерах равна модулю разности длины
тела в недеформированном состоянии и его длины в состоянии деформации.
в указанных выше примерах равна модулю разности длины
тела в недеформированном состоянии и его длины в состоянии деформации.
ПРИМЕР 21. Как изменится сила упругости резинового шнура, если его удлинение увеличить вдвое, оставив малым по сравнению с длиной шнура? Выберите правильный вариант ответа.
ОТВЕТ. Правильный вариант 1).
Действительно, по закону Гука с увеличением величины деформации пропорционально увеличивается и сила упругости.
ПРИМЕР 22. Спиральная пружина в недеформированном состоянии имеет длину 40 см. При уменьшении длины этой пружины на 3 см (сжатии) возникает сила упругости, равная 15 Н. Чему будет равна сила упругости при увеличении её длины (растяжении) на 2,3 см по сравнению с недеформированным состоянием?
РЕШЕНИЕ. В обоих случаях величины деформаций
пружины малы по сравнению с длиной пружины. Коэффициент упругости пружины
найдём с помощью закона Гука: 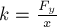 . Подставляя сюда
значения
. Подставляя сюда
значения 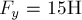 и
и 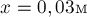 при сжатии пружины,
получим
при сжатии пружины,
получим 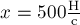 . Тогда искомая сила
. Тогда искомая сила 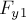 упругости при
растяжении
упругости при
растяжении 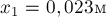 , будет равна
, будет равна 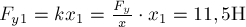 .
.
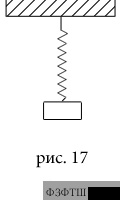
ПРИМЕР 23.
Тело массой 1 кг подвешено к
лёгкой длинной пружине, другой конец которой привязан к потолку комнаты
(рис.17). Система находится в равновесии относительно комнаты. Чему равна
деформация пружины, если коэффициент её упругости равен 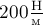 ?
?
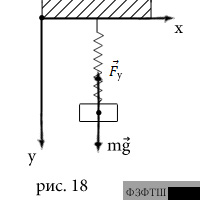
РЕШЕНИЕ. Говоря о том, что тело (или система
тел) находится в равновесии в некоторой инерциальной системе отсчёта,
подразумевают, что в этой системе отсчёта оно покоится. Свяжем инерциальную
систему отсчёта с потолком комнаты и рассмотрим силы, действующие на тело
(рис.18). В данном случае таких сил две: сила тяжести 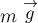 ,
действующая вертикально вниз, и сила упругости
,
действующая вертикально вниз, и сила упругости 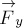 пружины. Так как
тело покоится, то его ускорение равно нулю. Следовательно, по 2-му закону
Ньютона и равнодействующая указанных сил равна нулю. Это возможно,
если
пружины. Так как
тело покоится, то его ускорение равно нулю. Следовательно, по 2-му закону
Ньютона и равнодействующая указанных сил равна нулю. Это возможно,
если 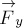 будет направлена вертикально вверх и по модулю равна силе
тяжести. Действительно, в проекциях на ось
будет направлена вертикально вверх и по модулю равна силе
тяжести. Действительно, в проекциях на ось 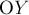 уравнение (1.1) даёт:
уравнение (1.1) даёт:
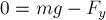 .
.
Отсюда 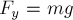 . Воспользовавшись
законом Гука рассчитаем величину деформации
пружины:
. Воспользовавшись
законом Гука рассчитаем величину деформации
пружины: 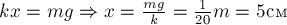 . По условию пружина
длинная и найденная деформация, следовательно, мала по сравнению с длиной
пружины. Значит применение закона Гука было оправданным. Условие лёгкости
пружины в данном случае означает, что её деформация вызвана только действием на
неё груза, а деформация пружины, вызванная действием собственной силы тяжести
пренебрежимо мала.
. По условию пружина
длинная и найденная деформация, следовательно, мала по сравнению с длиной
пружины. Значит применение закона Гука было оправданным. Условие лёгкости
пружины в данном случае означает, что её деформация вызвана только действием на
неё груза, а деформация пружины, вызванная действием собственной силы тяжести
пренебрежимо мала.
§11. Сила трения
Реальные движения тел, кроме, пожалуй, движения в безвоздушном пространстве, как правило, сопровождаются трением. Ниже пойдёт речь о трении, возникающем между соприкасающимися телами вследствие шероховатости их поверхности, и о сопротивлении (трении) среды (жидкости, газа), относительно которой движется тело.
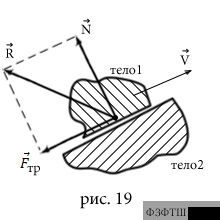
Пусть тело 1 движется относительно тела 2 (скользит
по телу 2), и пусть тело 2 действует на тело 1 с некоторой силой 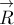 (сила
реакции опоры) (рис.19). При наличии трения, бывает удобно эту силу
разложить на две составляющие: силу
(сила
реакции опоры) (рис.19). При наличии трения, бывает удобно эту силу
разложить на две составляющие: силу 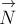 , перпендикулярную к поверхности
sконтакта тел (силу нормальной реакции опоры), и силу
, перпендикулярную к поверхности
sконтакта тел (силу нормальной реакции опоры), и силу 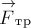 трения скольжения, направленную по касательной к поверхности контакта в сторону,
противоположную направлению движения тела 1 относительно тела 2. Заметим, что
по 3-му закону Ньютона такие же по модулю, но противоположные по направлению
силы, действуют на тело 2 со стороны тела 1. Указанное удобство заключается в
том, что при относительном скольжении тел модули этих составляющих связаны
между собой законом Кулона-Амонтона:
трения скольжения, направленную по касательной к поверхности контакта в сторону,
противоположную направлению движения тела 1 относительно тела 2. Заметим, что
по 3-му закону Ньютона такие же по модулю, но противоположные по направлению
силы, действуют на тело 2 со стороны тела 1. Указанное удобство заключается в
том, что при относительном скольжении тел модули этих составляющих связаны
между собой законом Кулона-Амонтона: 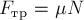 (7)
,где
(7)
,где 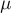 - положительный
коэффициент трения, зависящий от материала тел и свойств соприкасающихся
поверхностей.
- положительный
коэффициент трения, зависящий от материала тел и свойств соприкасающихся
поверхностей.
В дальнейшем при решении задач целесообразнее и
проще сразу изображать на рисунках силы 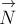 и
и 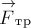 и не изображать
силу
и не изображать
силу 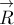 , являющуюся их суммой. Это помогает избежать путаницы и
загромождения рисунка. Но при этом надо всегда помнить и иметь в виду «причину
возникновения» указанных сил.
, являющуюся их суммой. Это помогает избежать путаницы и
загромождения рисунка. Но при этом надо всегда помнить и иметь в виду «причину
возникновения» указанных сил.
Часто при наличии внешнего воздействия на одно из
соприкасающихся тел их относительное движение (скольжение) отсутствует. Тогда
при разложении силы 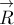 на указанные выше составляющие место силы трения
скольжения займёт сила трения покоя.
на указанные выше составляющие место силы трения
скольжения займёт сила трения покоя.
Для силы трения покоя закон (7) неприменим!
При неизменной силе 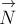 нормальной реакции
опоры модуль силы трения покоя может принимать значения от нуля до некоторого
максимального значения, слегка превышающего модуль силы трения
скольжения
нормальной реакции
опоры модуль силы трения покоя может принимать значения от нуля до некоторого
максимального значения, слегка превышающего модуль силы трения
скольжения 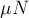 для соприкасающихся поверхностей (явление застоя). Однако
обычно максимальное значение силы трения покоя принимают
равным
для соприкасающихся поверхностей (явление застоя). Однако
обычно максимальное значение силы трения покоя принимают
равным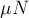 (пренебрегая явлением застоя).
(пренебрегая явлением застоя).
Если на тело 1 действует некоторая внешняя
сила  , стремящаяся сдвинуть его относительно тела 2, то эту силу
также можно представить как сумму двух сил:
, стремящаяся сдвинуть его относительно тела 2, то эту силу
также можно представить как сумму двух сил: 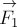 , параллельной
поверхности соприкосновения тел (или направленной по касательной к этой
поверхности), и
, параллельной
поверхности соприкосновения тел (или направленной по касательной к этой
поверхности), и 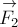 , перпендикулярной поверхности соприкосновения.
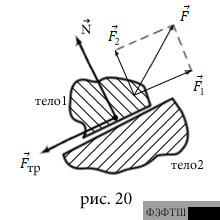
Модуль силы трения покоя равен модулю параллельной (касательной)
составляющей
, перпендикулярной поверхности соприкосновения.
Модуль силы трения покоя равен модулю параллельной (касательной)
составляющей 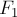 внешней силы
внешней силы  , а направление силы трения покоя
противоположно направлению этой составляющей (рис.20).
, а направление силы трения покоя
противоположно направлению этой составляющей (рис.20).
При изменении силы  с увеличением
модуля её касательной составляющей увеличивается и модуль силы трения покоя до
тех пор, пока не станет равным максимальному значению
с увеличением
модуля её касательной составляющей увеличивается и модуль силы трения покоя до
тех пор, пока не станет равным максимальному значению 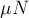 (см.
выше). Дальнейшее увеличение касательной составляющей уже не приведёт к
увеличению силы трения. Сила трения уже на сможет уравновешивать
силу
(см.
выше). Дальнейшее увеличение касательной составляющей уже не приведёт к
увеличению силы трения. Сила трения уже на сможет уравновешивать
силу 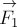 , и тогда начнётся скольжение (относительное движение) тела 1
по телу 2. При этом сила трения станет силой трения скольжения, с постоянным
модулем, равным
, и тогда начнётся скольжение (относительное движение) тела 1
по телу 2. При этом сила трения станет силой трения скольжения, с постоянным
модулем, равным 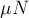 .
.
ПРИМЕР 24.
На брусок массой  ,
лежащий на горизонтальной поверхности стола, начинает действовать
сила
,
лежащий на горизонтальной поверхности стола, начинает действовать
сила  , параллельная поверхности стола. Нарисуйте график
зависимости модуля силы трения, действующей на брусок, от модуля силы.
, параллельная поверхности стола. Нарисуйте график
зависимости модуля силы трения, действующей на брусок, от модуля силы.
РЕШЕНИЕ. Кроме силы  и силы
трения на брусок также действуют сила нормальной реакции опоры со стороны стола
и сила тяжести
и силы
трения на брусок также действуют сила нормальной реакции опоры со стороны стола
и сила тяжести 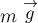 (рис.21).
(рис.21).
Если сила 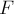 равна нулю, то и сила трения
равна нулю (нет воздействия, стремящегося сдвинуть брусок). При этом сила
реакции опоры
равна нулю, то и сила трения
равна нулю (нет воздействия, стремящегося сдвинуть брусок). При этом сила
реакции опоры 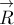 суть сила нормальной реакции
суть сила нормальной реакции 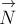 .
.
Далее, при увеличении модуля 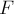 возникает
сила трения, которая до тех пор, пока не началось движение бруска по столу,
является силой трения покоя. Её модуль
возникает
сила трения, которая до тех пор, пока не началось движение бруска по столу,
является силой трения покоя. Её модуль 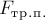 также увеличивается. При этом
выполняется равенство:
также увеличивается. При этом
выполняется равенство: 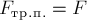 (*)
(*)
Когда модуль 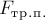 станет равен
станет равен 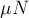 , то в
соответствии с (*) в этот момент модуль
, то в
соответствии с (*) в этот момент модуль 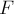 также равен
также равен 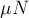 .
.
При дальнейшем увеличении модуля силы 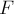 возникает проскальзывание бруска по столу, и сила трения является уже силой
трения скольжения. Её модуль остаётся постоянным и равным
возникает проскальзывание бруска по столу, и сила трения является уже силой
трения скольжения. Её модуль остаётся постоянным и равным 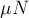 ,
независимо от величины внешней силы.
,
независимо от величины внешней силы.
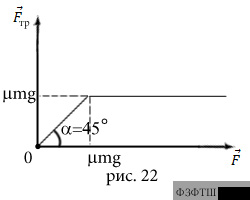
Уравнение 2-го закона Ньютона в проекциях на ось 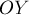 для тела даёт:
для тела даёт: 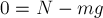
Здесь учтено, что проекция
ускорения бруска на вертикальное направление равна нулю. Отсюда 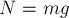 . График зависимости
. График зависимости 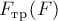 изображён на рис.22.
изображён на рис.22.
ПРИМЕР 25.
На гладкой горизонтальной поверхности
стола лежит доска массой 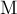 , по которой скользит брусок массой
, по которой скользит брусок массой  .
Чему равно ускорение доски при её движении вдоль стола,
если
.
Чему равно ускорение доски при её движении вдоль стола,
если 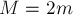 , а коэффициент трения бруска о доску равен
, а коэффициент трения бруска о доску равен 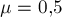 ?
?
РЕШЕНИЕ. Силы, действующие на брусок и доску
показаны на рис.23. Смысл обозначений ясен из рисунка. Силы 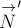 и
и 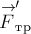 действуют на доску со стороны бруска и по 3-му закону Ньютона равны по модулю и
противоположны по направлению силам
действуют на доску со стороны бруска и по 3-му закону Ньютона равны по модулю и
противоположны по направлению силам 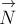 и
и 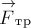 соответственно. По
условию поверхность стола гладкая и, следовательно, трения между доской и
столом нет.
соответственно. По
условию поверхность стола гладкая и, следовательно, трения между доской и
столом нет.
Пусть искомое ускорение доски равно 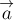 . Его
может сообщить доске только сила трения скольжения
. Его
может сообщить доске только сила трения скольжения 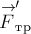 как
единственная сила, направленная вдоль стола. Остальные силы, действующие на
доску, направлены вертикально, а их сумма равна нулю, так как в этом
направлении доска не движется.
как
единственная сила, направленная вдоль стола. Остальные силы, действующие на
доску, направлены вертикально, а их сумма равна нулю, так как в этом
направлении доска не движется.
Уравнение 2-го закона Ньютона в проекциях на ось 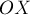 имеет вид:
имеет вид:
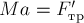 (**).
Здесь
(**).
Здесь 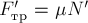 , где
, где 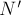 сила
нормальной реакции опоры, действующая на доску со стороны бруска. По 3-му
закону Ньютона N' = N. В свою очередь
сила
нормальной реакции опоры, действующая на доску со стороны бруска. По 3-му
закону Ньютона N' = N. В свою очередь 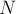 найдём, записав для
бруска уравнение 2-го закона Ньютона в проекциях на ось
найдём, записав для
бруска уравнение 2-го закона Ньютона в проекциях на ось 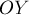 :
: 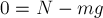 .
.
Здесь учтено, что брусок в этом направлении не
движется и его ускорение равно нулю. Таким образом 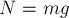 и,
следовательно,
и,
следовательно, 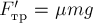 . Тогда с учётом (**) находим
. Тогда с учётом (**) находим
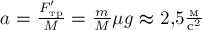
Если тело может катиться по той или иной поверхности, то из-за деформации материала этой поверхности под катящимся телом возникает сила трения качения, которая прямо пропорциональна силе нормальной реакции опоры со стороны поверхности и обратно пропорциональна внешнему радиусу катящегося тела. При этом указанная деформация поверхности может быть не заметной глазу. Обычно сила трения качения намного меньше силы трения скольжения и ей, поэтому, пренебрегают.
При поступательном движении тела в жидкости или газе возникает сила сопротивления среды, зависящая от скорости движения тела относительно среды. Эта сила может быть прямо пропорциональна как самой указанной скорости, так и её квадрату (в зависимости от конкретных условий задачи). Однако в любом случае направление силы сопротивления среды противоположно направлению вектора скорости тела относительно среды.
ПРИМЕР 26.
Мячик массой 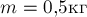 бросили
вертикально вниз с большой высоты в безветренную погоду. При подлёте к
поверхности земли он падает с постоянной скоростью. Чему равна сила
сопротивления воздуха перед ударом мяча о землю?
бросили
вертикально вниз с большой высоты в безветренную погоду. При подлёте к
поверхности земли он падает с постоянной скоростью. Чему равна сила
сопротивления воздуха перед ударом мяча о землю?
РЕШЕНИЕ. В процессе падения на мяч действуют
сила тяжести 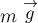 , направленная вертикально вниз и сила сопротивления
воздуха
, направленная вертикально вниз и сила сопротивления
воздуха 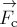 , направленная в сторону, противоположную скорости мяча,
т.е. - вертикально вверх (рис.24). Величина силы сопротивления на начальном
этапе движения возрастает с увеличением модуля скорости падения мяча (т.к. по
условию ветра нет, то скорость мяча относительно воздуха равна скорости мяча
относительно земли). В некоторый момент времени скорость падения увеличится
настолько, что сила сопротивления воздуха сравняется по модулю с силой тяжести
мяча. В этот момент равнодействующая рассматриваемых сил становится равной
нулю, а так как других сил в задаче нет (архимедовой силой пренебрегаем), то
ускорение мяча также становится равным нулю, и, начиная с этого момента, при
своём дальнейшем движении, мяч падает с постоянной скоростью.
, направленная в сторону, противоположную скорости мяча,
т.е. - вертикально вверх (рис.24). Величина силы сопротивления на начальном
этапе движения возрастает с увеличением модуля скорости падения мяча (т.к. по
условию ветра нет, то скорость мяча относительно воздуха равна скорости мяча
относительно земли). В некоторый момент времени скорость падения увеличится
настолько, что сила сопротивления воздуха сравняется по модулю с силой тяжести
мяча. В этот момент равнодействующая рассматриваемых сил становится равной
нулю, а так как других сил в задаче нет (архимедовой силой пренебрегаем), то
ускорение мяча также становится равным нулю, и, начиная с этого момента, при
своём дальнейшем движении, мяч падает с постоянной скоростью.
Уравнение 2-го закона Ньютона в проекциях на ось 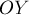 ,
записанное для мяча перед ударом о поверхность земли, даёт:
,
записанное для мяча перед ударом о поверхность земли, даёт:
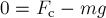 .
.
Отсюда искомая сила сопротивления
воздуха 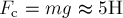
§12 Вес тела
Определение 9. Силу, с которой тело вследствие его притяжения к Земле, действует на опору или на подвес, называют весом тела.
ПРИМЕР 27.
Брусок массой 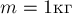 , лежит
на наклонной плоскости (рис.25). Проскальзывание отсутствует. Чему равен вес
бруска?
, лежит
на наклонной плоскости (рис.25). Проскальзывание отсутствует. Чему равен вес
бруска?
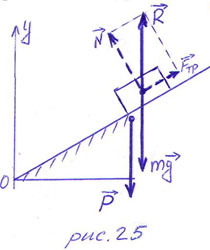
РЕШЕНИЕ. На брусок действуют сила
тяжести 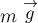 и сила реакции опоры
и сила реакции опоры 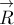 со стороны наклонной
плоскости (рис.25). Напомним, что сила
со стороны наклонной
плоскости (рис.25). Напомним, что сила 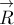 равна сумме сил нормальной
реакции опоры и силы трения (в данном случае - силы трения покоя). На рис.25
эти силы показаны пунктиром.
равна сумме сил нормальной
реакции опоры и силы трения (в данном случае - силы трения покоя). На рис.25
эти силы показаны пунктиром.
По 3-му закону Ньютона брусок действует на наклонную
плоскость с силой 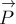 , равной по модулю силе
, равной по модулю силе 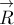 и противоположно
её направленной. Иными словами:
и противоположно
её направленной. Иными словами: 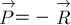 .
Ещё раз отметим, что сила
.
Ещё раз отметим, что сила 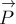 приложена к наклонной плоскости.
приложена к наклонной плоскости.
Напомним, что конкретные точки приложения всех указанных сил мы не уточняем.
Так как брусок покоится, то его ускорение равно
нулю, и, следовательно, уравнение 2-го закона Ньютона для бруска, записанное в
проекциях на вертикальную ось 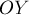 , даёт:
, даёт:
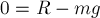
Откуда 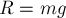 и,
следовательно,
и,
следовательно, 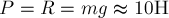
Таким образом, вес бруска равен по
модулю 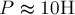 , направлен вертикально вниз и приложен к опоре – к
наклонной плоскости.
, направлен вертикально вниз и приложен к опоре – к
наклонной плоскости.
Вес тела является результатом взаимодействия тела и опоры (или подвеса). Он определяется совокупностью всех действующих на тело сил (а не только силы тяжести). Так вес тела в жидкости или газе меньше, чем в вакууме из-за действия выталкивающей (архимедовой) силы. Кроме того, вес тела зависит от ускорения, с которым движутся совместно опора (или подвес) и тело.
ПРИМЕР 28.
Тело массой  стоит на полу
лифта, движущегося с ускорением
стоит на полу
лифта, движущегося с ускорением 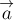 , направленным вертикально вниз
(рис.26). Чему равен вес тела?
, направленным вертикально вниз
(рис.26). Чему равен вес тела?
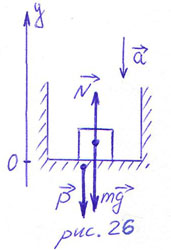
РЕШЕНИЕ. Опорой для тела служит пол лифта.
Относительно движение тела и опоры отсутствует. На тело действуют сила
тяжести 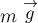 и сила нормальной реакции опоры
и сила нормальной реакции опоры 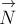 со стороны пола
лифта (трения нет и, значит,
со стороны пола
лифта (трения нет и, значит, 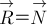 ).
На опору со стороны тела действует вес тела
).
На опору со стороны тела действует вес тела 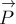 .
По 3-му закону Ньютона
.
По 3-му закону Ньютона 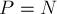 ,
а направление
,
а направление 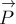 противоположно направлению
противоположно направлению 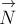 (рис. 26).
(рис. 26).
Тело движется вместе с лифтом с ускорением 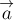 .
По 2-му закону Ньютона для тела имеем:
.
По 2-му закону Ньютона для тела имеем: 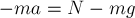
Отсюда 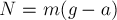 .
Следовательно, модуль веса тела равен
.
Следовательно, модуль веса тела равен 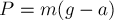 .
Вес тела приложен к лифту. Конкретные точки приложения сил не уточняем.
.
Вес тела приложен к лифту. Конкретные точки приложения сил не уточняем.
Заметим, что при 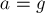 , вес тела (и сила
реакции опоры) обратится в нуль. Наступит так называемое состояние
невесомости. Но сила тяжести, равная по модулю
, вес тела (и сила
реакции опоры) обратится в нуль. Наступит так называемое состояние
невесомости. Но сила тяжести, равная по модулю 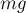 , будет
по-прежнему действовать на тело.
, будет
по-прежнему действовать на тело.
Если бы ускорение 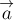 было направлено
вертикально вверх, то вес тела был бы равен
было направлено
вертикально вверх, то вес тела был бы равен 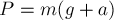 . Убедитесь в этом самостоятельно.
. Убедитесь в этом самостоятельно.
ПРИМЕР 29.
Шарик массой  подвешен на
лёгкой нерастяжимой нити, другой конец которой прикреплён к потолку вагона,
движущегося горизонтально с ускорением
подвешен на
лёгкой нерастяжимой нити, другой конец которой прикреплён к потолку вагона,
движущегося горизонтально с ускорением 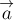 (рис.27). Чему равен вес
шарика?
(рис.27). Чему равен вес
шарика?
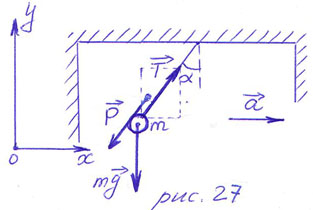
РЕШЕНИЕ. Нить служит для шарика подвесом. При
движении вагона с ускорением 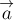 нить отклоняется на некоторый
угол
нить отклоняется на некоторый
угол 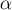 от вертикали (рис.27). На шарик действуют сила
тяжести
от вертикали (рис.27). На шарик действуют сила
тяжести 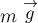 и сила натяжения нити
и сила натяжения нити 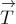 .
По 3-му закону Ньютона вес шарика равен
.
По 3-му закону Ньютона вес шарика равен 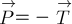 и приложен к нити.
На рис.27 сила
и приложен к нити.
На рис.27 сила 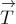 для наглядности изображена параллельно нити и как бы «висит» в воздухе.
для наглядности изображена параллельно нити и как бы «висит» в воздухе.
Поскольку шарик покоится относительно вагона, то
ускорение шарика также равно 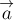 . В проекциях на оси
. В проекциях на оси 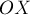 и
и 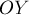 имеем
для шарика уравнения:
имеем
для шарика уравнения:
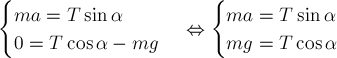
Возведём оба уравнения в квадрат, сложим и
воспользуемся основным тригонометрическим тождеством. Тогда
получим 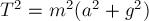 , откуда
, откуда 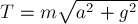 и, следовательно,
и, следовательно, 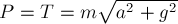 .
Вес шарика действует вдоль нити в направлении «от точки крепления к потолку» под углом
.
Вес шарика действует вдоль нити в направлении «от точки крепления к потолку» под углом 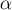 к вертикали, причём
к вертикали, причём 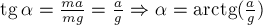 .
.
ПРИМЕР 30. Вертикальная стенка движется горизонтально с ускорением, толкая перед собой кубик массой m (рис.28). Кубик покоится относительно стенки. Чему равен вес тела?
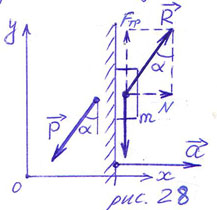
РЕШЕНИЕ. Опорой для кубика служит стенка.
Относительное движение отсутствует, значит кубик также движется горизонтально с
ускорением 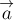 .
На кубик действуют сила тяжести
.
На кубик действуют сила тяжести 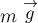 и
сила реакции опоры со стороны стенки
и
сила реакции опоры со стороны стенки 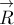 (рис.28). Напоминаем, что
сила
(рис.28). Напоминаем, что
сила 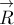 может быть заменена двумя силами
может быть заменена двумя силами 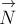 и
и 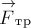 (в данном случае имеет место трение покоя). На рисунке эти силы показаны пунктиром.
(в данном случае имеет место трение покоя). На рисунке эти силы показаны пунктиром.
Вес кубика приложен к стенке и
равен 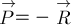 .
.
По 2-му закону Ньютона для кубика система уравнений
движения в проекциях на оси 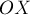 и
и 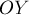 имеет вид:
имеет вид: 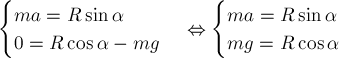 .
.
Откуда по аналогии с предыдущим примером
находим 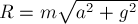 . Следовательно модуль веса
кубика
. Следовательно модуль веса
кубика 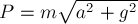 . Направление вектора
. Направление вектора 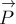 составляет
с вертикалью угол
составляет
с вертикалью угол 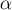 такой, что
такой, что 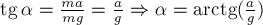
§13. Примеры комбинированных динамических задач
ЗАДАЧА 1.
Два прямоугольных бруска массами 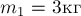 и
и 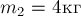 связаны лёгкой нерастяжимой нитью и лежат на гладкой горизонтальной поверхности
стола (рис.29а). На первый брусок начинает действовать горизонтально направленная
сила
связаны лёгкой нерастяжимой нитью и лежат на гладкой горизонтальной поверхности
стола (рис.29а). На первый брусок начинает действовать горизонтально направленная
сила 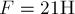 . Определите ускорение брусков и силу натяжения
нити.
. Определите ускорение брусков и силу натяжения
нити.
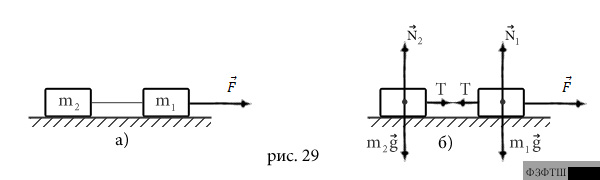
РЕШЕНИЕ. Ускорения, с которыми движутся оба
бруска одинаковы, так как нить нерастяжима. Силы, действующие на брусок,
показаны на рис.29б. Силы натяжения нити 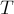 , действующие на бруски,
одинаковы, так как нить лёгкая. Уравнения 2-го закона Ньютона для первого и
второго брусков в проекциях на ось
, действующие на бруски,
одинаковы, так как нить лёгкая. Уравнения 2-го закона Ньютона для первого и
второго брусков в проекциях на ось 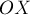 имеют вид соответственно:
имеют вид соответственно:
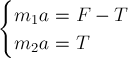 .
.
Отсюда следует, что 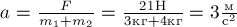
ЗАДАЧА 2.
Система состоит из одного подвижного и
одного неподвижного блока. К оси подвижного блока подвешен груз
массой 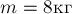 . С каким ускорением будет подниматься груз, если
за конец нити, перекинутый через неподвижный блок, тянуть вертикально вниз с
постоянной силой
. С каким ускорением будет подниматься груз, если
за конец нити, перекинутый через неподвижный блок, тянуть вертикально вниз с
постоянной силой 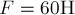 (рис.30а)? Массы блоков и нитей малы,
нити нерастяжимы, трением пренебречь.
(рис.30а)? Массы блоков и нитей малы,
нити нерастяжимы, трением пренебречь.

РЕШЕНИЕ. Действующие в системе силы показаны
на рис.30б. Так как массы блоков малы, то можно считать, что сила 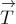 натяжения нити, к которой прикреплён груз, действующая на подвижный блок
уравновешивается двумя равными силами
натяжения нити, к которой прикреплён груз, действующая на подвижный блок
уравновешивается двумя равными силами 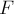 , действующими на подвижный
блок вдоль другой нити с обеих сторон. Так как масса нити, удерживающей груз,
мала, то такая же по модулю сила действует на груз. Так как масса нити,
перекинутой через блоки, и массы блоков малы, а трением в блоках можно пренебречь,
то сила натяжения этой нити одинакова по всей её длине и равна
силе
, действующими на подвижный
блок вдоль другой нити с обеих сторон. Так как масса нити, удерживающей груз,
мала, то такая же по модулю сила действует на груз. Так как масса нити,
перекинутой через блоки, и массы блоков малы, а трением в блоках можно пренебречь,
то сила натяжения этой нити одинакова по всей её длине и равна
силе  , с которой нить тянут за свободный конец. Разумеется, силы
натяжения для каждой нити свои.
, с которой нить тянут за свободный конец. Разумеется, силы
натяжения для каждой нити свои.
По 2-му закону Ньютона для подвижного блока
(его масса 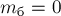 ) имеем в проекциях на ось
) имеем в проекциях на ось 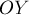 :
:
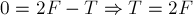
Аналогично для груза:
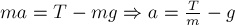
С учётом найденной силы 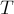 ,
получим для ускорения груза
,
получим для ускорения груза 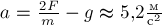
Заметим, что поскольку нити нерастяжимы, то ускорение груза равно ускорению подвижного блока и в два раза меньше ускорения свободного конца нити, перекинутой через блоки (покажите это самостоятельно).
ЗАДАЧА 3.
Шайба, брошенная вдоль наклонной
плоскости, скользит по ней, двигаясь вверх, а затем возвращается к месту
броска. Наклонная плоскость составляет с горизонтом угол 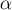 .
Коэффициент трения скольжения между шайбой и плоскостью равен
.
Коэффициент трения скольжения между шайбой и плоскостью равен 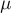 .
Чему равно ускорение шайбы при движении а) вверх по наклонной плоскости, б)
вниз по наклонной плоскости?
.
Чему равно ускорение шайбы при движении а) вверх по наклонной плоскости, б)
вниз по наклонной плоскости?
РЕШЕНИЕ. а) Силы, действующие на шайбу при
движении вверх, показаны на рис.31а. Там же изображены оси координат
инерциальной системы отсчёта. Ускорение шайбы направим вдоль наклонной
плоскости вниз. По 2-му закону Ньютона для шайбы имеем в проекциях на оси
координат: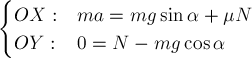
В первом уравнении мы учли, что сила трения скольжения равна 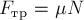
Из написанных уравнений находим: 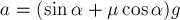
б) При движении шайбы вниз по наклонной плоскости на
неё действуют те же силы, только направление силы трения скольжения поменялось
на противоположное, и теперь эта сила направлена вдоль наклонной плоскости вверх.
Ускорение шайбы направим по-прежнему вдоль наклонной плоскости вниз. По 2-му
закону Ньютона для шайбы имеем в проекциях на те же координатные оси (рис.31б): 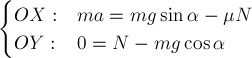
И вновь в первом уравнении мы учли,
что 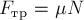 . Отсюда находим
. Отсюда находим 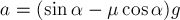
ЗАДАЧА 4. (МФТИ)
Автомобиль, трогаясь с места,
равномерно набирает скорость, двигаясь по горизонтальному участку дороги,
представляющему собой дугу окружности с углом 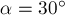 (рис.32а). Радиус
окружности
(рис.32а). Радиус
окружности 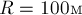 . С какой максимальной скоростью
. С какой максимальной скоростью 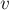 автомобиль
может выехать на прямой участок пути? Коэффициент трения колёс о дорогу
автомобиль
может выехать на прямой участок пути? Коэффициент трения колёс о дорогу 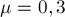
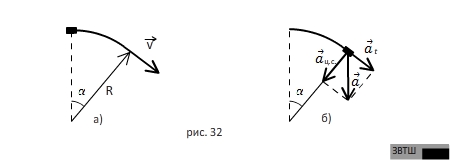
РЕШЕНИЕ. Ускорение в горизонтальной плоскости
автомобилю сообщает сила трения. Остальные силы (тяжести и нормальной реакции
опоры) направлены вертикально. Максимальное ускорение, которое может развивать
автомобиль определяется максимальной силой трения (покоя) колёс о поверхность
дороги: 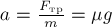
В данном случае ускорение автомобиля есть векторная
сумма нормального (центростремительного) ускорения 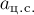 и тангенциального
(касательного) ускорения
и тангенциального
(касательного) ускорения 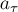 (рис.32б). Центростремительное ускорение
«отвечает» за изменение направления скорости и определяется формулой
(рис.32б). Центростремительное ускорение
«отвечает» за изменение направления скорости и определяется формулой 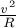 .
Оно достигает своего максимального значения в конце
пути, когда скорость автомобиля максимальна. Тангенциальное ускорение
«отвечает» за изменение модуля скорости и по условию задачи постоянно (т.е.
движение равноускоренное). Следовательно, скорость, которую будет иметь
автомобиль в конце разгона, равна
.
Оно достигает своего максимального значения в конце
пути, когда скорость автомобиля максимальна. Тангенциальное ускорение
«отвечает» за изменение модуля скорости и по условию задачи постоянно (т.е.
движение равноускоренное). Следовательно, скорость, которую будет иметь
автомобиль в конце разгона, равна 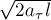 , где
, где 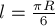 и,
значит,
и,
значит, 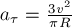 . Учитывая, что по теореме
Пифагора
. Учитывая, что по теореме
Пифагора 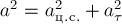 , и подставляя в это соотношение
значения
, и подставляя в это соотношение
значения 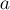 ,
, 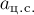 и
и 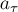 ,
получим
,
получим 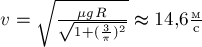
ЗАДАЧА 5. (МФТИ)
На внутреннюю поверхность полого шара радиуса 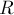 ,
вращающегося вокруг вертикальной оси с постоянной угловой скоростью
,
вращающегося вокруг вертикальной оси с постоянной угловой скоростью 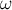 ,
находится маленькая шайба А(рис.33а).
Считая угол
,
находится маленькая шайба А(рис.33а).
Считая угол 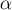 известным, найти минимальный коэффициент
трения, при котором шайба не сорвётся вниз.
известным, найти минимальный коэффициент
трения, при котором шайба не сорвётся вниз.
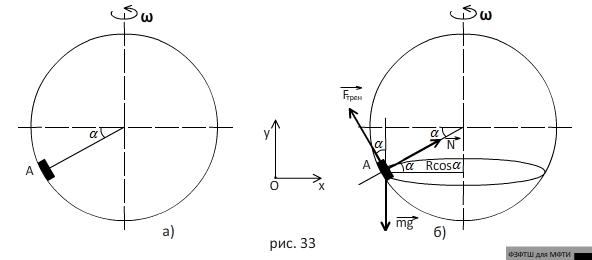
РЕШЕНИЕ. На шайбу действуют
(рис.33б): 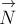 - сила нормальной реакции опоры (шара),
- сила нормальной реакции опоры (шара), 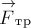 -
сила трения, касательная к поверхности шара,
-
сила трения, касательная к поверхности шара, 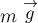 - сила тяжести.
Максимальная сила трения (сила трения скольжения) равна
- сила тяжести.
Максимальная сила трения (сила трения скольжения) равна 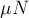 ,
где
,
где 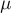 - коэффициент трения. Шайба вращается в горизонтальной плоскости
вокруг вертикальной оси. Центростремительное ускорение направлено горизонтально
к оси и по модулю равно
- коэффициент трения. Шайба вращается в горизонтальной плоскости
вокруг вертикальной оси. Центростремительное ускорение направлено горизонтально
к оси и по модулю равно 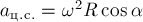 . По 2-му закону Ньютона для
шайбы имеем в проекциях на выбранные оси координат:
. По 2-му закону Ньютона для
шайбы имеем в проекциях на выбранные оси координат: 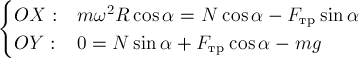
Отсюда находим:
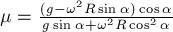
ЗАДАЧА 6.
Автомобиль массой 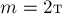 движется со скоростью
движется со скоростью
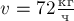 по выпуклому мосту, имеющему радиус кривизны
по выпуклому мосту, имеющему радиус кривизны 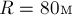 .
С какой силой
.
С какой силой  автомобиль давит на мост перпендикулярно
поверхности моста в его середине? С какой минимальной скоростью
автомобиль давит на мост перпендикулярно
поверхности моста в его середине? С какой минимальной скоростью 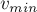 должен двигаться автомобиль для того, чтобы в верхней точке он перестал
оказывать давление на мост?
должен двигаться автомобиль для того, чтобы в верхней точке он перестал
оказывать давление на мост?
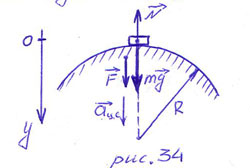
РЕШЕНИЕ. Силы, действующие на автомобиль в
середине моста, показаны на рис.34. По третьему закону Ньютона искомая сила
давления  равна по модулю силе нормальной реакции моста
равна по модулю силе нормальной реакции моста 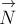 .
По 2-му закону Ньютона для автомобиля имеем в проекциях на вертикальную ось
.
По 2-му закону Ньютона для автомобиля имеем в проекциях на вертикальную ось 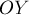 :
: 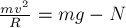 ,
где
,
где 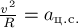 - центростремительное ускорение.
- центростремительное ускорение.
Отсюда 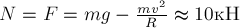
Сила 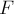 станет равной нулю
при
станет равной нулю
при 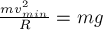 . Следовательно,
. Следовательно, 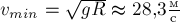
ЗАДАЧА 7.
Шарик, подвешенный к потолку на
верёвке, движется в горизонтальной плоскости по окружности, отстоящей от
потолка на расстояние 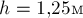 .
Найдите период
.
Найдите период 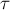 обращения камня.
обращения камня.
РЕШЕНИЕ. Силы, действующие на шарик показаны
на рис.35, где 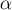 - угол, который верёвка составляет с вертикалью.
Центростремительное ускорение шарика равно
- угол, который верёвка составляет с вертикалью.
Центростремительное ускорение шарика равно 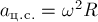 .
Второй закон Ньютона для шарика имеет вид в проекциях на оси:
.
Второй закон Ньютона для шарика имеет вид в проекциях на оси:
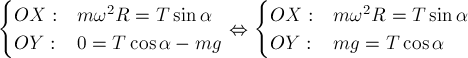 ,где
,где 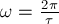 -
угловая скорость шарика, а
-
угловая скорость шарика, а  - его масса. Отсюда получим
- его масса. Отсюда получим 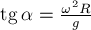
Учитывая, что 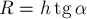 и,
значит,
и,
значит, 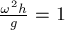 , получим
, получим